Optuna
samplers
Alan Barzilay
Grid Search
Impractical most of the time.
Wastes too much time in low performance regions.
Random Search
Same issues as Grid Search, but a step in the right direction.
Links
Tree-structured Parzen Estimator
TPE
- Single objective default
- Flexible, fast and reliable
- Scary name, simple idea
Tip: set multivariate to True
Random Exploration
1.
Partitioning the Search Space and Parzen Estimation
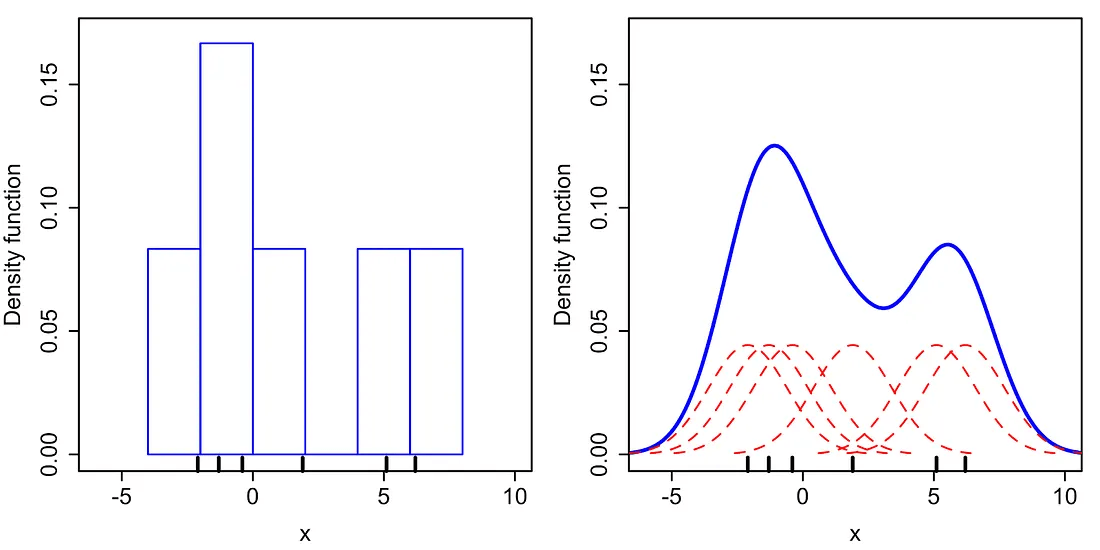
l(x) groups the top γ% performing hyperparameter combinations.
l(x) is "good" and g(x) is "bad".
2.
Determining the Next “Best” Hyperparameters to Test
Test the maximum of g(x)/l(x), rinse repeat.
3.
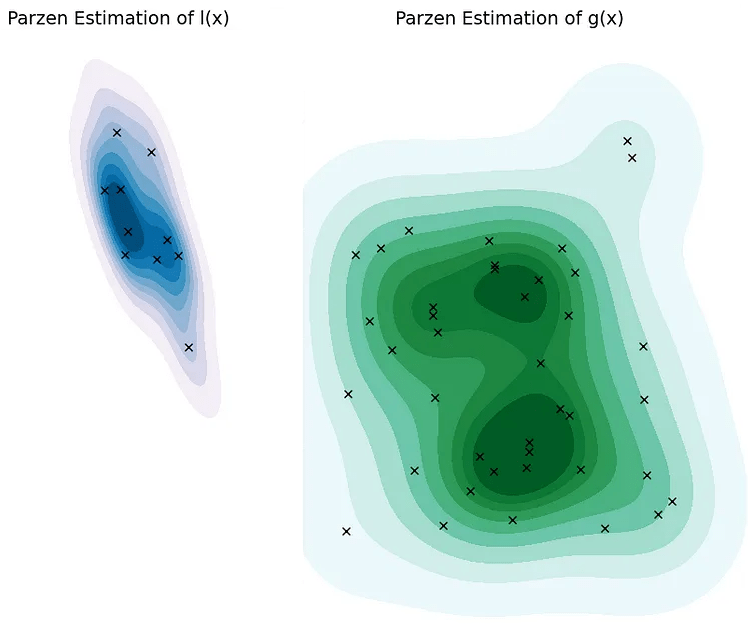
The Parzen window estimator is a statistical model for density estimation, which is also called the kernel density estimator (KDE). In the TPE algorithm, Parzen window estimators are used to estimate the densities of good hyperparameters \(l(x)\) and bad hyperparameters \(g(x)\).
Intuitively speaking, the Parzen window estimator (in right figure) is a smoothed version of the histogram of relative frequency (in the left figure).
TPE - Interesting Refs
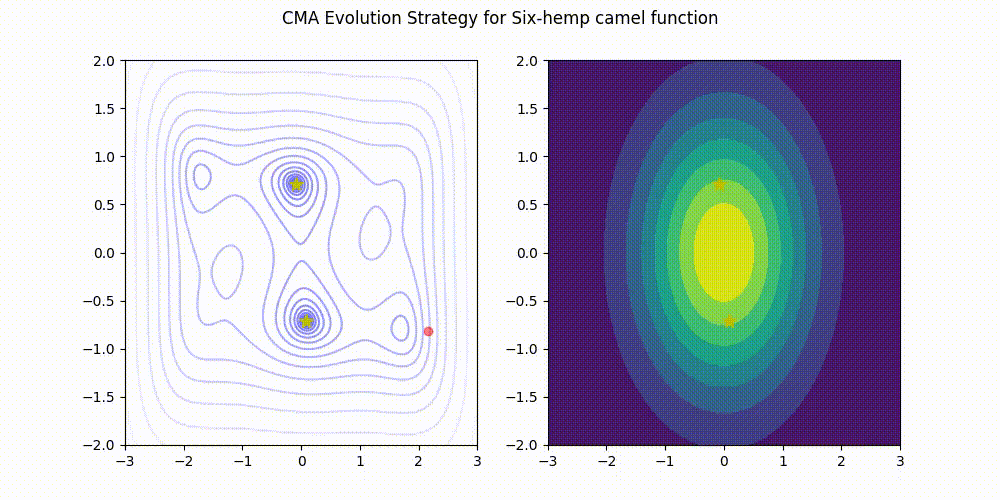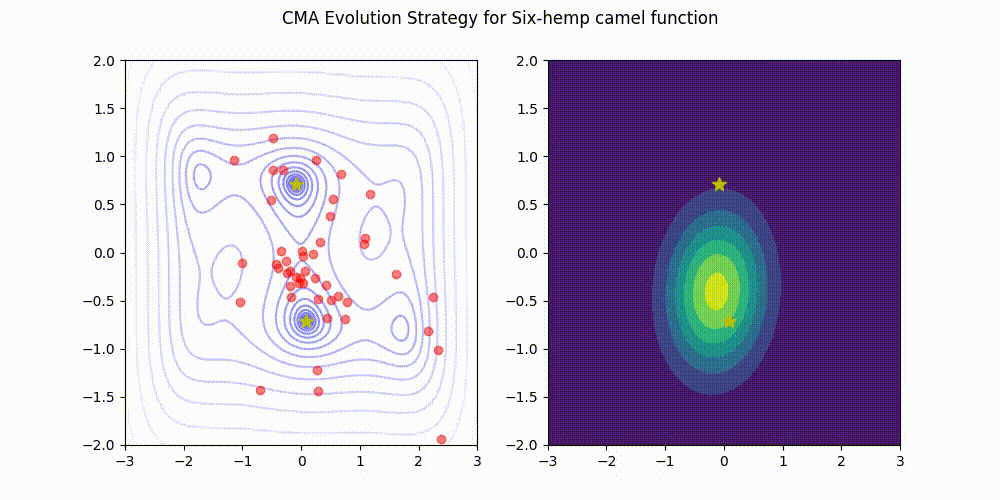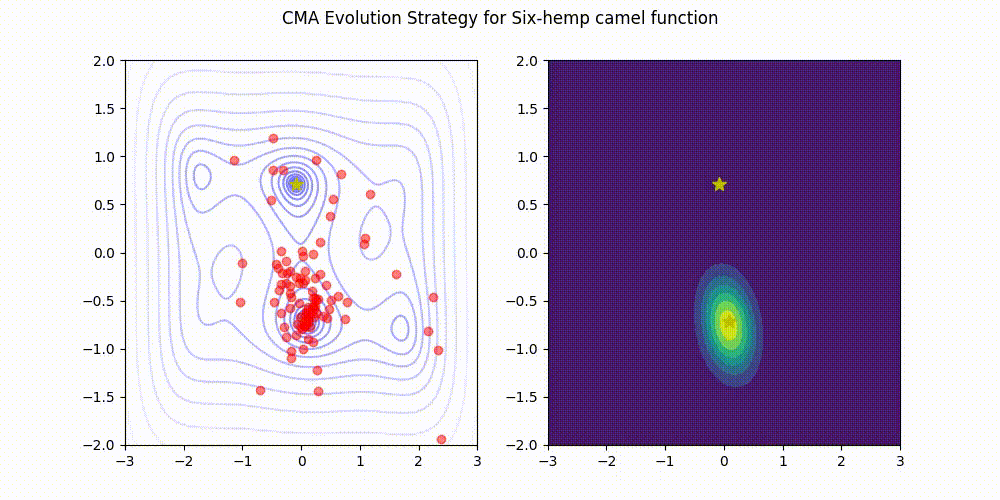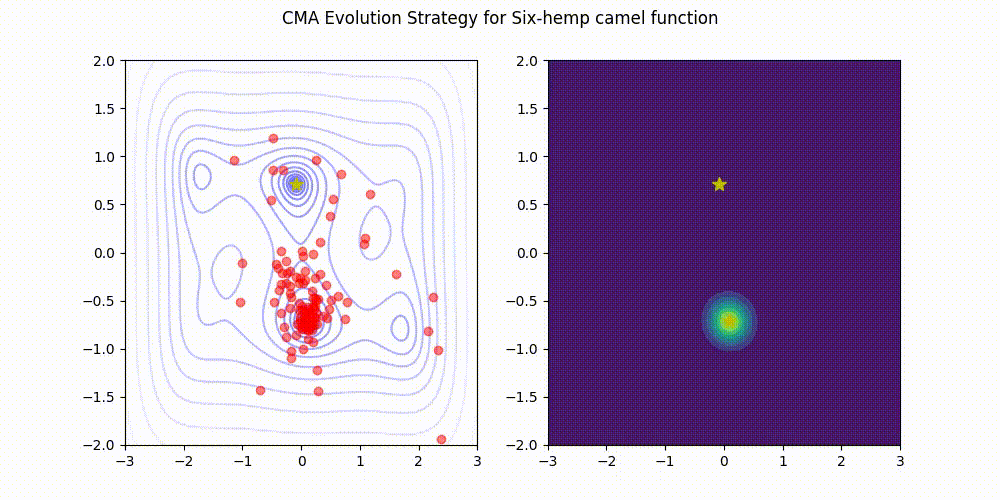
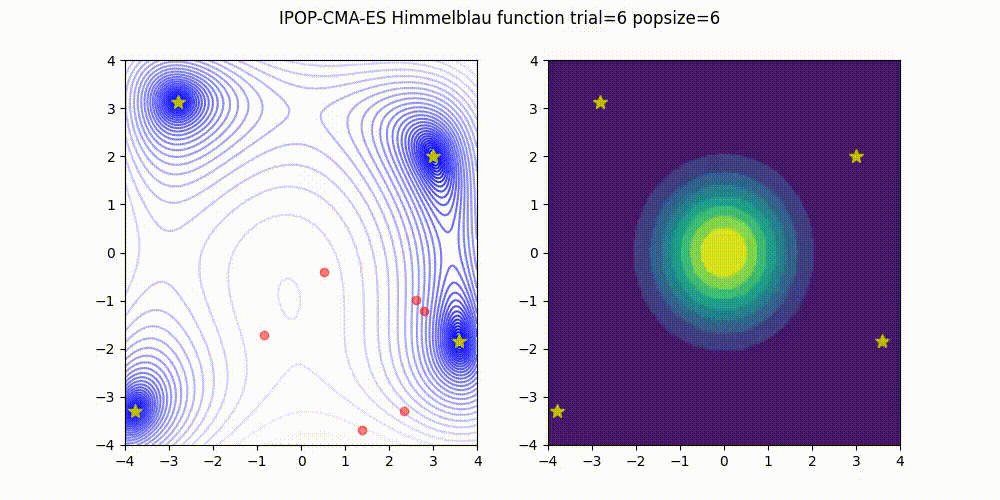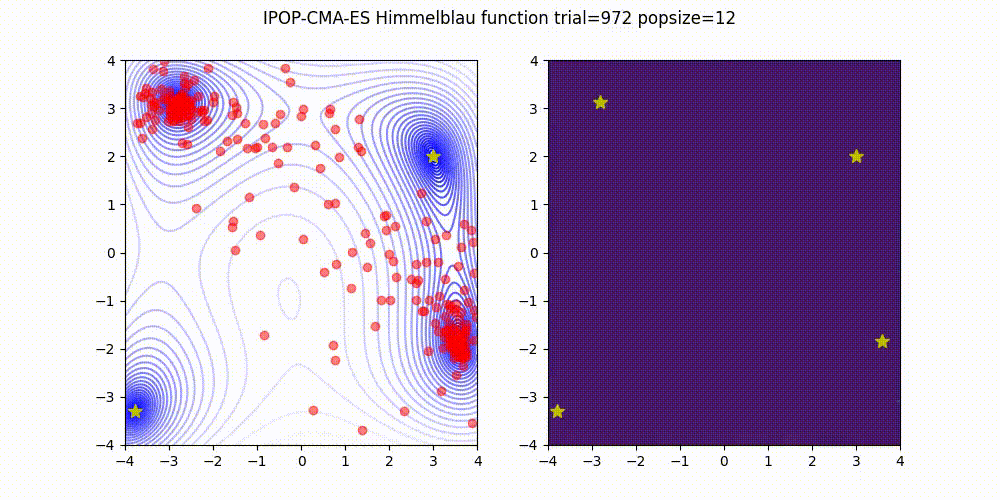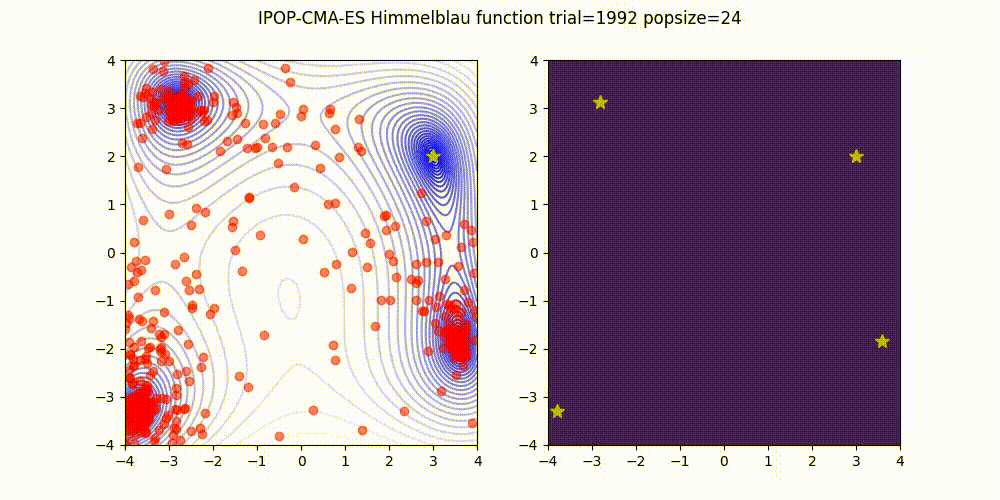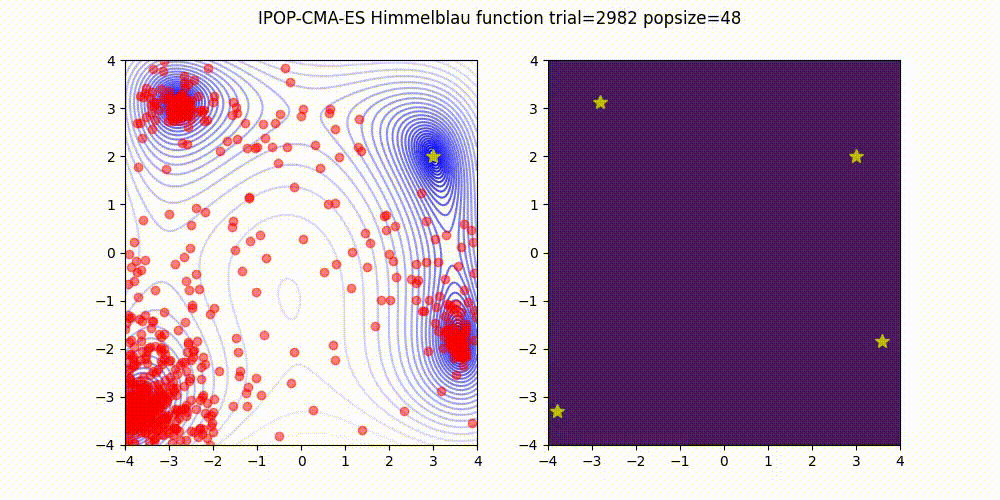
Covariance Matrix Adaptation Evolution Strategy
CMA-ES
Fits a gaussian in the search space that, when sampled, results in a good set of hyperparameters.
More intuitively, slide and stretch a gaussian across the surface until it gets "stuck" in a minima. Resembles gradient descent.
Covariance Matrix Adaptation Evolution Strategy
Q: What if it gets stuck in a local minima?
A: Restart it
CMA-ES
Covariance Matrix Adaptation Evolution Strategy
You could also Warm Start it, use margins, use and adaptive learning rate, diagonalize the covariance matrix or use any other of its many variations (most of which supported natively by Optuna).
Not as flexible or fast as TPE (e.g. there is no support for categorical variable or constraints)
CMA-ES
CMA ES - Interesting Refs
Gaussian Process
GP
This is a big one, there are entire courses on the subject.
Let's focus on how it contrasts with other samplers instead of really explaining the algorithm minute inner workings.
Gaussian Process
GP
The biggest difference between GP and other samplers is on the approach of looking for new points to test.
With TPE and CMA-ES we take a number of random trials as a warm start and based on them we try new points we believe will perform well.
Gaussian Process
GP
GP in contrast, utilizes an acquisition function to balance the trade-off between exploration (testing new regions of the state space) and exploitation (sampling new points from a known good region).
Every time GP tests a new point in its exploration state, it will pick a set of hyper-parameters that maximizes "information" on the search space and minimizes uncertainty regions so that it can exploit good regions with high confidence.
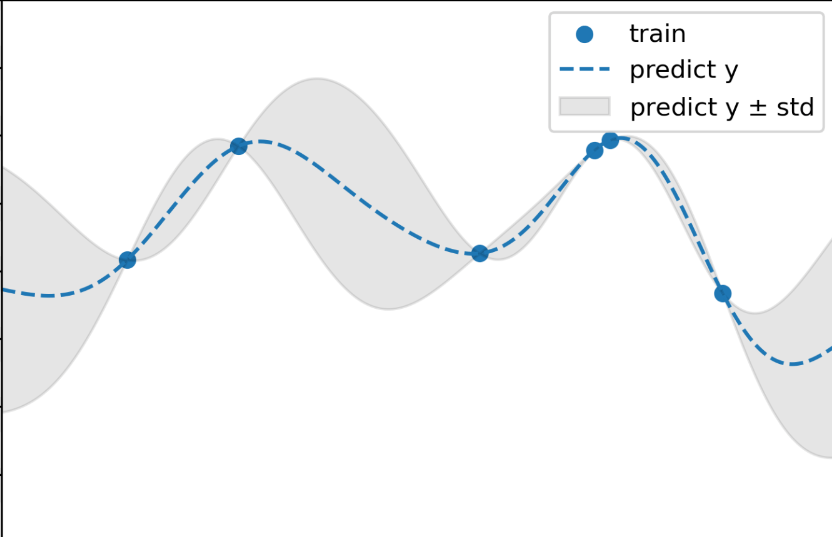
Gaussian Process
GP
However, this process is extremely computationally expensive as the number of trials increases being \(O(d^3)\), where \(d\) is the number of complete trails.
That's why a common strategy is to use it only for the initial exploration of the search space where it is still computationally viable and then switch to another sampler.
There is a lot of good materials online (and a lot of imprecise ones) so I won't further add to the noise. For the interested reader, here are some curated and rigorous references on the subject.
For those looking to fine tune their usage of GP, the key "levers" are kernels (or covariance functions), acquisition functions and priors.
GP - References
GP - References
Non-dominated Sorting
NSGA
Genetic Algorithm
- Rank and sort population according to objective metrics
- Take the best and create new population
- Rinse and repeat
Non-dominated Sorting
NSGA
Genetic Algorithm
Non-dominated Sorting
NSGA
Genetic Algorithm
Steps:
- Binary tournament selection
- Crossover
- Mutation
\(P_t\) generates \(Q_t\) and together they form \(R_{t+1}\), from which \(P_{t+1}\) will be selected
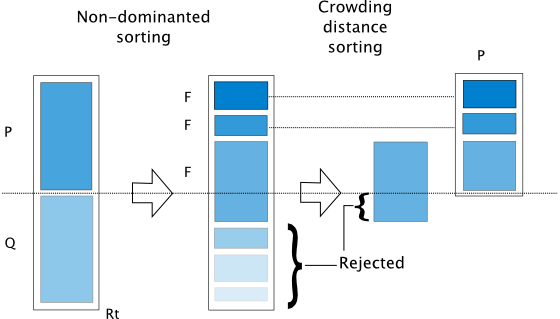
Non-dominated Sorting
NSGA
Genetic Algorithm
Pareto Front
NSGA
Non-dominated Sorting
A Pareto Onion
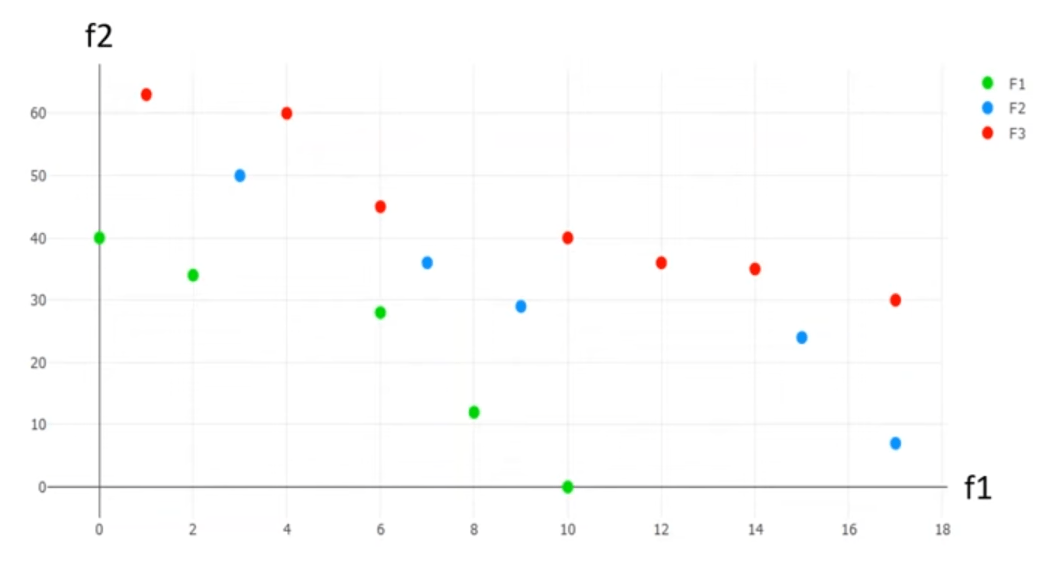
NSGA
Genetic Algorithm
Non-dominated Sorting
NSGA
Genetic Algorithm
Q: How to ensure "genetic" diversity?
A: Crowding Distance
Q: How do we select points from the last layer?
A: Crowding Distance
Q:How do we break a rank tie in the tournament selection?
A: Crowding Distance
Non-dominated Sorting
NSGA
Genetic Algorithm
Crowding Distance: Sorting the last Front
NSGA
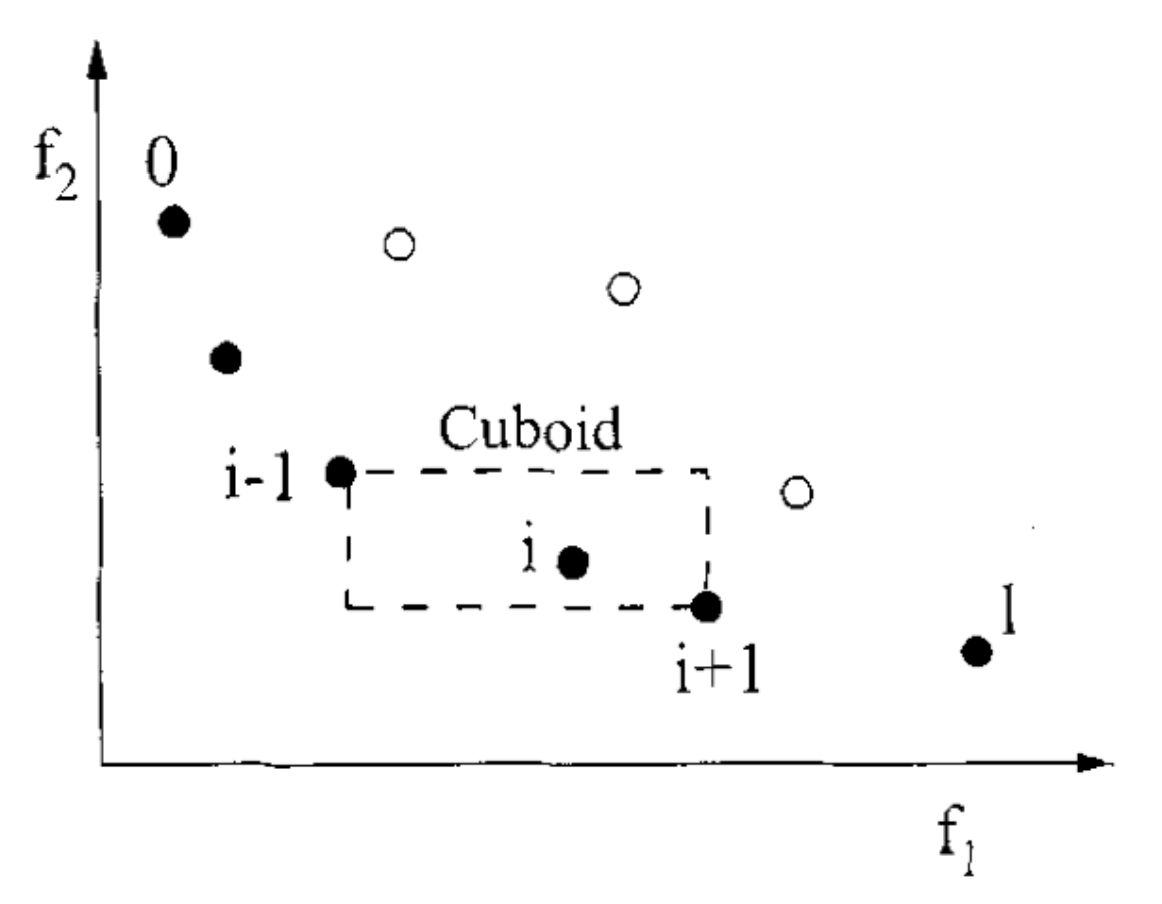
- Crowding distance is the Manhatan/L1 distance between "neighbors"
- By taking the points with the biggest crowding distance we essentially select a spread-out set of points
- "Border" of the frontier gets ∞ distance
The curse of dimensionality
NSGA
With more than 3 dimensions we start to struggle with:
- Visualization
- Computational Complexity
- Sparsity
With NSGA II in particular:
- Crowding Distance becomes too costly
- A large fraction of the population is non-dominated
- Two distant parent solutions are likely to produce offspring solutions that are also distant from parents
The curse of dimensionality
The proportion of non-dominated solutions in a randomly chosen set of objective vectors becomes exponentially large with an increase of number of objectives.
How do we deal with this?
The non-dominated solutions occupy most of the population slots.
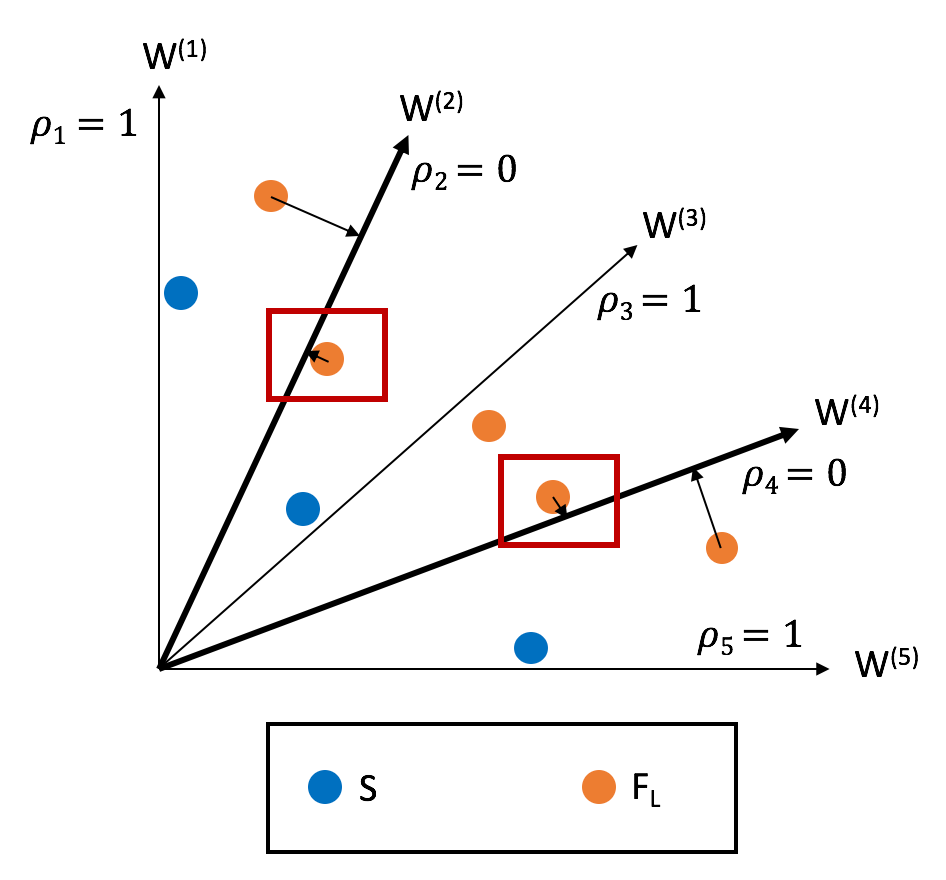
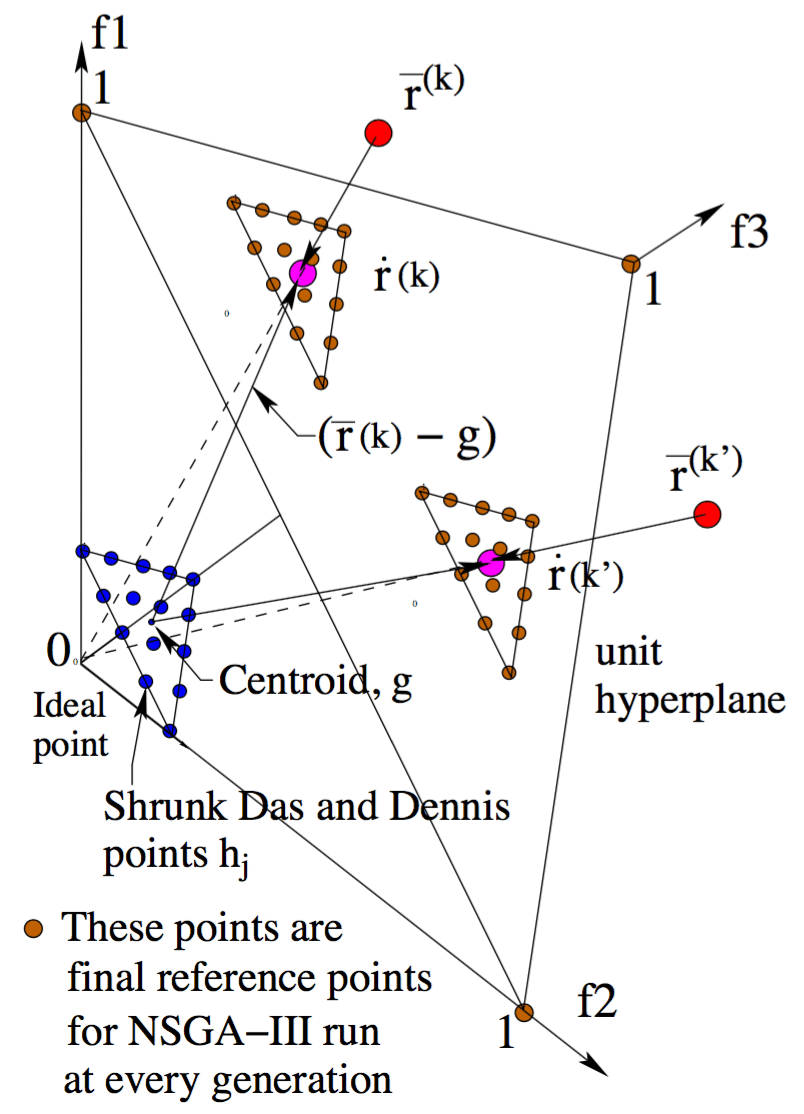
Reference Directions
Splits the objective space with vectors (usually uniformly distributed) that define reference directions W
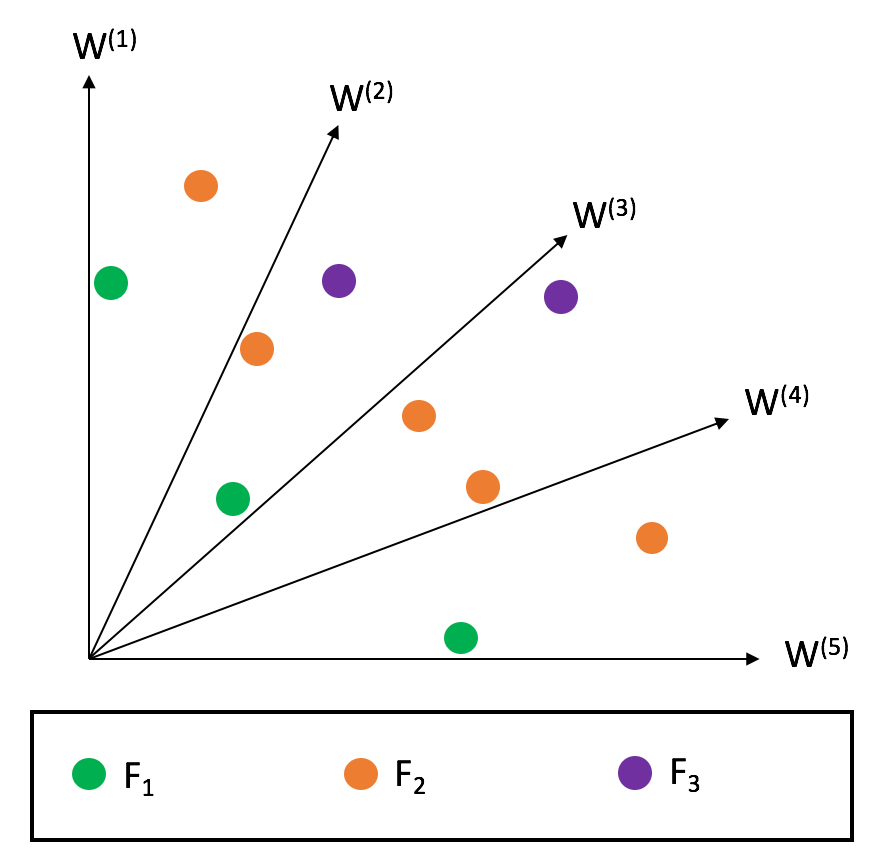
NSGA III
The split is made in a manner to balance the population proximity across reference directions.
\(S\): "Previous" Pareto fronts
\(F_L\): Frontier to be split
\(\rho_i\): number of points associated with direction
\(W_i\): Reference Direction \(i\)
FAQ and miscellaneous things
Q: What if <insert niche use case or clever heuristic>?
A: NSGA III is a variation of NSGA II and both have a ton of variations, which have variations of their own. I suggest taking a look at the existing literature but be advised that you will probably have quickly diminishing returns. Maybe try another family of algorithms?
FAQ and miscellaneous things
Q: Could you further elaborate on reference directions?
A: I could, but this is outside of the scope of this presentation. The fact that I find the topic extremely boring is totally unrelated and bears no weight in this decision.
FAQ and miscellaneous things
Q: What about NSGA I?
A: 2 is bigger than 1 so obviously NSGA I sucks and doesn't matter, stop asking stupid questions
FAQ and miscellaneous things
Q: What about those reference directions?
A: Here are some cool pictures and quotes, plz leave me alone, I'm begging you
emphasizes population members that are non-dominated, yet close to a set of supplied reference points. LISPECTOR, Clarice
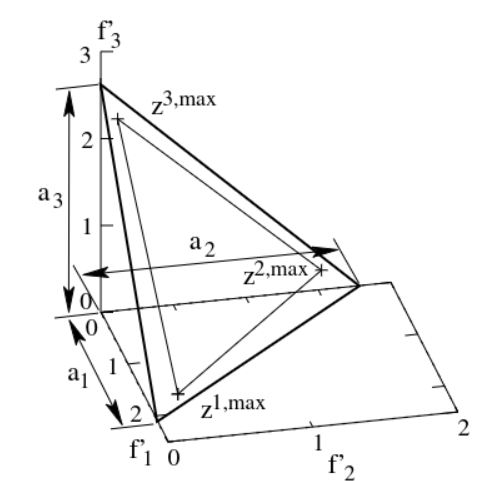
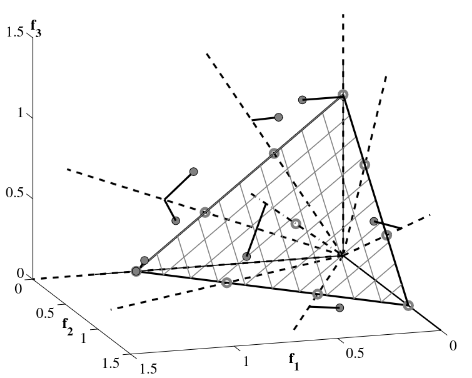
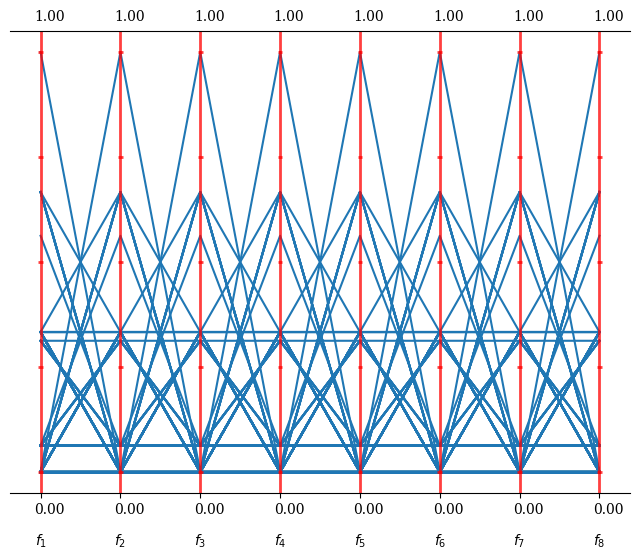
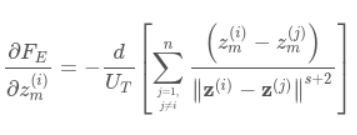
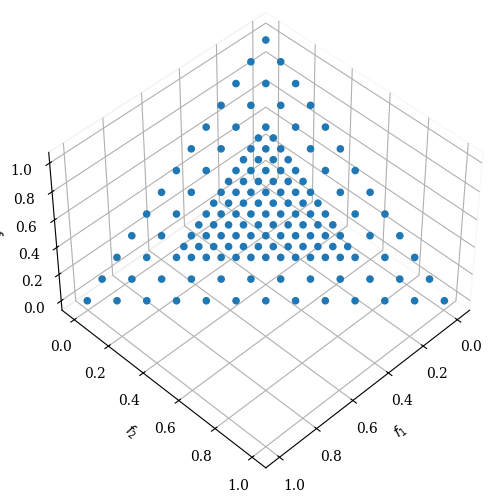
(...) we use Das and Dennis’s [48] systematic approach that places points on a normalized hyper-plane – a (M − 1)- dimensional unit simplex – which is equally inclined to all objective axes.
DENNIS & DAS... i guess?
Riesz s-Energy
NSGA - Interesting Refs
Really cool and all that, but...
Which one should I use?
Defaults are pretty solid but, maybe try the new auto sampler?
It chooses the "ideal" sampler for your conditions and swaps between them in a smart and efficient manner. However, as of the moment of writing it isn't battle tested.
while budget >0:
if multi-objective:
if conditional_params → TPE
elif few_trials_completed: # few trials: <250
if ≥4 objectives or categorical → TPE
else → GP
else:
if <4 objectives → NSGA-II
else → NSGA-III
else:
if categorical or conditional → TPE
elif few_trials_completed → GP
elif no_constraints → CMA-ES
else → TPE
budget-=1
'%20xmlns:inkscape='http://www.inkscape.org/namespaces/inkscape'%20xmlns:sodipodi='http://sodipodi.sourceforge.net/DTD/sodipodi-0.dtd'%20xmlns='http://www.w3.org/2000/svg'%20xmlns:svg='http://www.w3.org/2000/svg'%3e%3cdefs%20id='defs1'%20/%3e%3csodipodi:namedview%20id='namedview1'%20pagecolor='%23ffffff'%20bordercolor='%23000000'%20borderopacity='0.25'%20inkscape:showpageshadow='2'%20inkscape:pageopacity='0.0'%20inkscape:pagecheckerboard='0'%20inkscape:deskcolor='%23d1d1d1'%20inkscape:zoom='41.2'%20inkscape:cx='9.9878641'%20inkscape:cy='10'%20inkscape:window-width='2560'%20inkscape:window-height='1052'%20inkscape:window-x='0'%20inkscape:window-y='0'%20inkscape:window-maximized='1'%20inkscape:current-layer='svg1'%20/%3e%3cpath%20id='path1901'%20d='m1467.7%200h-1347.9c-64.5%200-119.2%2051-119.2%20113.8v1353.4c0%2062.9%2035.9%20113.9%20100.4%20113.9h1347.9c64.5%200%20133.4-51%20133.4-113.9v-1353.4c0-62.8-50-113.8-114.6-113.8z'%20style='fill:none'%20/%3e%3cpath%20id='path1903'%20d='m%201582.3,113.8%20v%201353.4%20c%200,62.9%20-68.9,113.9%20-133.4,113.9%20H%20101%20c%20-64.5,0%20-100.4,-51%20-100.4,-113.9%20V%20113.8%20C%200.6,51%2055.3,0%20119.8,0%20h%201347.9%20c%2064.6,0%20114.6,51%20114.6,113.8%20z%20M%20603.1,1355.2%20h%20226%20V%20993.6%20c%200,-126.2%2054.1,-203.1%20167.7,-203.1%2093.6,0%20133.6,87.9%20133.6,188%20v%20376.7%20h%20225.9%20V%20937.3%20c%200,-223.6%20-63.5,-344.4%20-291,-344.4%20-118.6,0%20-214.4,59.4%20-246.9,117.9%20h%20-2.3%20V%20602.3%20h%20-213%20z%20m%20-376.6,0%20h%20226%20V%20602.3%20h%20-226%20z%20M%20439.4,239.1%20c%20-26.5,-26.5%20-62.4,-41.3%20-99.9,-41.3%20-37.4,0%20-73.3,14.9%20-99.8,41.3%20-26.5,26.5%20-41.3,62.4%20-41.3,99.8%200,37.4%2014.9,73.3%2041.3,99.8%2026.5,26.5%2062.5,41.3%2099.9,41.3%2037.4,0%2073.4,-14.9%2099.8,-41.3%2026.5,-26.5%2041.4,-62.4%2041.3,-99.9%200,-37.4%20-14.9,-73.3%20-41.3,-99.7%20z'%20style='fill:currentColor'%20/%3e%3c/svg%3e)